As discussed in Article 1, Deep Learning models require a mechanism to update the model parameters automatically. The Stochastic gradient descent (SGD) is the mathematical foundation of this mechanism.

The following diagram, visually describes the SGD method. dl model

Image Source: Fastai Book, Chapter 4

The above model has been explained in greater detail in the proceeding subsections:

Step 1: Initialize Weights

  • Gradient descent method involves starting at a random point on a function
  • Hence, in DL, this involves initializing model parameters (weights) to random values

  • The following image, is an example of a random point being selected in a curve

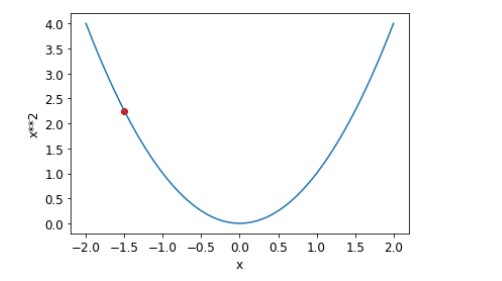
    step1_sgd

    Image Source: Fastai Book, Chapter 4

Step 2: Predict Outcome Using Weights

  • Using weights, an expected result can be predicted

Step 3: Measure Loss

  • Need to measure the effectiveness of the weights
  • Using a function, we can quantitatively describe the performance (level of loss)
  • Function will return:
    1. Small number - if the loss is minimal
    2. Large number - if the loss is significant
  • Gives DL a way of understanding how well the current model is performing

Step 4: Step through with Gradient

  • As weight parameters are adjusted, change in gradient (derivative of loss) can be measured
  • Correlates weight values with respect to model performance
  • Will indicate the winning direction, and amount to adjust weight parameters by

  • Idea of ‘descent’ is to go in opposite direction of gradient to optimise performance

  • An example image has been provided below, which depicts the loss being measured with respect to a model parameter (weight) using the gradient of the curve

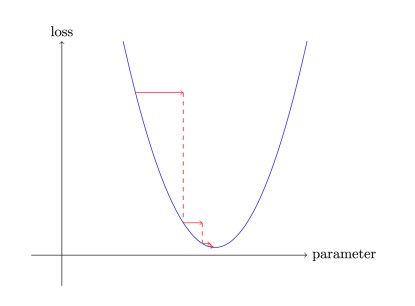
    step3_sgd

    Image Source: Fastai Book, Chapter 4

Reference List

https://nbviewer.org/github/fastai/fastbook/blob/master/04_mnist_basics.ipynb