Foundation of Neural Networks
1. Neural Network Concept
As discussed by IBM, neural networks are a fundamental component of deep learning models. They consists of node layers. Each node is designated a certain weight and threshold. As shown below, the input layers are related to the output layers via multiple hidden layers:
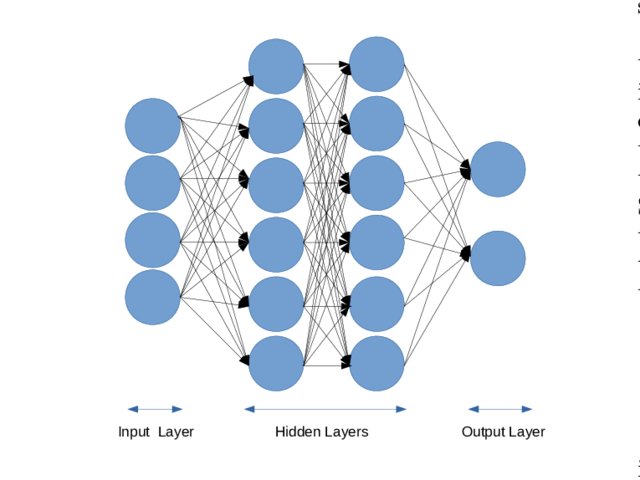
From paper “Using Deep Learning to Localize Gravitational Wave Sources”
2. Neural Model
As shown in the above image, a neuron (node) is fed inputs. Additionally, each node has an inherent weight ($ w $). The multiplication of the input with its corresponding weight, plus the addition of a bias ($b$), yields an expression for the output of a neuron.
Output of a Neuron
\[O_{i,j} = x_{i,k} w_{k,j} + b_{j}\]We can deduce from this equation, neuron output is inherently matrix multiplication.
from Fast AI Textbook - Chapter 17
3. Broadcasting
Tensors (matrices) will not always have the same rank. In a situation where two tensors in an operation do not have the same shape, broadcasting is used to make sure they are compatible with one another.
There are several types of broadcasting:
3.1 Broadcasting with a Scalar
Consider when an array and scalar are both involved in an operation.
a = [1, 2, 3]
b = 2
c = a * b
In this situation, broadcasting rules stipulate the scalar must be extended into an array of the same size as the matrix/array, as shown in the conceptual diagram below:
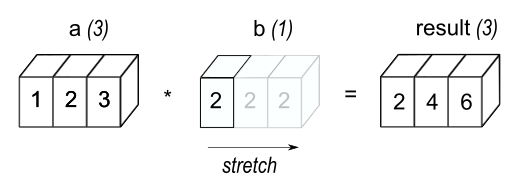
3.2 Vector to Matrix
3.2.1 Matrix & Matrix Broadcasting Rules
3.2.1.1 Rules
Tensors are compatible for arithmetic operations when:
- Dimensions are identical, or
- Dimensions of one of the matrices is 1
Provided these conditions are met, the output matrix:
“Will have same number of dimensions as the input array with the greatest number of dimensions” (Numpy, 2023)
3.2.1.2 Example:
We can demonstrate this principle in the following example, with the multiplication of a 4D matrix and 3D matrix:
Matrix A: 4 x 1 x 3 x 1
Matrix B: ? x 2 x 1 x 5
Result C: 4 x 2 x 3 x 5
As higlighted in green the size of each dimension in the resulting matrix corresponds to the largest size of the input matrices.
Also take note of the ‘?’ in Matrix B. In such a situation, where the dimension is unknown, it is assumed to be size 1.
A visual depiction of this broadcasting technique has been shown below:
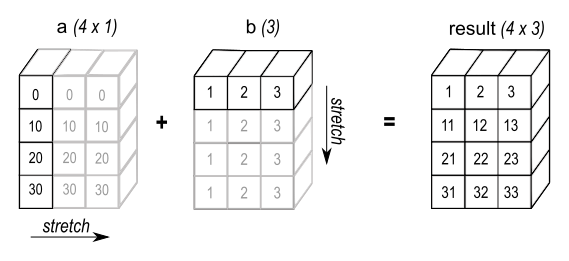
Image from Numpy Documentation
Reference List
https://numpy.org/doc/stable/user/basics.broadcasting.html
https://nbviewer.org/github/fastai/fastbook/blob/master/17_foundations.ipynb
https://www.researchgate.net/publication/335855384_Using_Deep_Learning_to_Localize_Gravitational_Wave_Sources/figures?lo=1
https://www.ibm.com/topics/neural-networks